Esthétopies
Variétés d'espaces sensibles
Les espaces se construisent et se découvrent. Espaces physiques ou imaginaires.
Un espace vit s’il est visité. Il peut l’être pour son utilité ; mais aussi pour sa beauté et ses mystères. Il peut être parcouru pour sa fertilité : une entrée vers d’autres espaces, d’autres curiosités. Aimés pour être familiers et étranges, sauvages et omniprésents ou classiques et bouleversants... La découverte d’un nouvel espace peut être dérangeante.
Une réalité que les mathématiciens et les artistes côtoient. Cette exposition propose des expériences sensibles avec des espaces nés de l’imaginaire mathématique.
Les espaces mathématiques travaillés ici sont similaires à notre espace physique. Ils se nomment variétés de dimension 3. Ils sont pour l’espace euclidien ce qu’une surface est pour un plan, ce qu’une courbe est pour une droite.
Les lois de la physique se transcrivent naturellement aux variétés, elles permettent de définir les trajectoires de la lumière et celle du son. D’une variété à l’autre, les trajectoires sont différentes, déformées par la courbure de chacun des espaces. Les perspectives visuelles et réverbérations sonores y sont différentes.
La plupart de ces espaces n’ont jamais été visités. Pour cette exposition, des recherches mathématiques et numériques ont été menées pour s’y immerger. Elles révèlent celles qui classifient toutes les variétés de dimension 3. Elles forment la matière brute des oeuvres exposées.
Crédits
1. Théorèmes de classification des espaces: Moebius, Jordan, 1866. Klein, Poincaré, Koebe, 1907. Milnor, 1967. Thurston,Perelman, 2002.
2. Sélection de modèles mathématiques de l’IHP.
3. Courtes vidéos sur la définition et la construction de variétés, Pierre Berger et Pierre-Yves Fave, 2013.
4. Paysages des huit géométries de Thurston, Pierre Berger, 2015-2016.
5. Conversation dans plusieurs espaces, Pierre Berger, Sergio Krakowski, Jimena Royo-Letelier, 2016-2017.
6. Navigation dans les sommes connexes, Pierre Berger, 2016-2017.
7. Plongement sonore de l’Institut Henri Poincaré dans l’espace R3=Z3, Pierre Berger, Vincent Martial, Jimena Royo-Letelier, 2017.
Une exposition coordonnée par Pierre Berger.
Sonorités d’espaces
On peut comprendre un espace par ses sonorités. Si l’on tape sur un tambour, il émet un son qui dépend de sa forme et de sa matière. Si l’on parle dans un espace, le son s’y propage et s’y réverbère pour être entendu d’une certaine façon. Ces sonorités en disent long sur la géométrie de l’espace... mais ne révèlent pas tout.
La physique sait modéliser les sons d’un espace physique par une équation. Cette même équation
peut être appliquée à des espaces imaginaires. Pour certains espaces mathématiques,
l’équation du son se résout explicitement en utilisant des théories mathématiques majeures
du 19ème siècle. Aussi les ordinateurs sont assez puissants pour interagir phoniquement avec
ces espaces. Les installations présentées ici sont les premières à le faire.
Les espaces choisis sont des espaces de l’imaginaire mathématique, des variétés d’espaces.
Par exemple, l’espace R3=Z3 est un cube dont les faces opposées sont collées, alors que l’espace
S3 désigne un espace dont tous les points éloignés se rapprochent d’un unique point.
Ces espaces imaginaires ont été munis d’une matière choisie pour ses qualités acoustiques.

Paysage d'espaces
On peut comprendre un espace en regardant à l’intérieur. C’est ce que nous faisons avec les
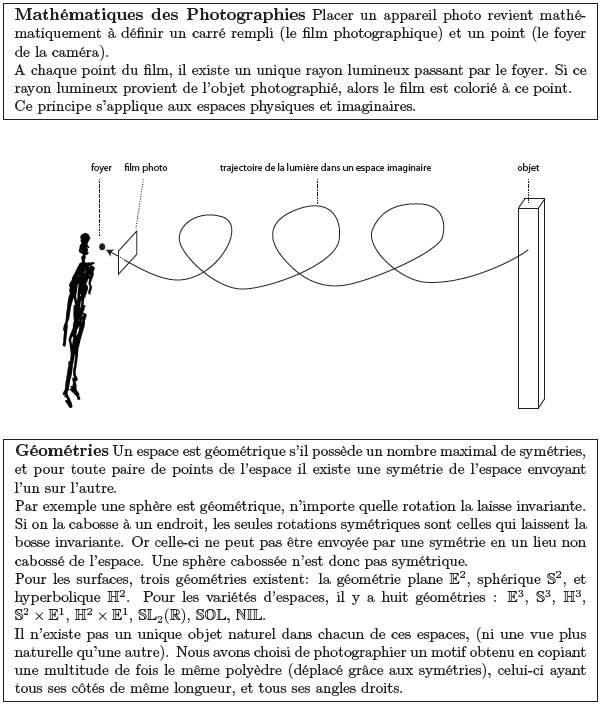
variétés d’espaces. Pour y voir, il faut y mettre de la lumière et y placer un objet (sinon
l’espace est vide et obscur).
En général, les variétés d’espaces ne sont pas plates. Ses courbures forment de multiples
lentilles optiques, elles déforment les trajectoires de la lumière en des courbes non rectilignes.
Dans beaucoup d’espaces, la lumière peut s’enrouler ou spiraler, ou encore former une courbe
extrêmement sauvage. Les photographies dans ces espaces imaginaires reflètent la trajectoire
de la lumière et révèlent ainsi leur géométrie.